In my 2nd edition there is a table of tangents, sines and cosines and radians on pp 301-308 for 0* to 360*. Example tangent on 25* = 0.46631
The bad news, I've forgotten 90% of my geometry and I don't what to do with this!
Thanks for looking.
An example of what I'm talking about can be found at:
http://www.mathsisfun.com/algebra/trig-finding-side-right-triangle.html 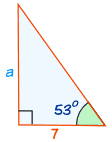
The third to the last example on that page is the formula I use most often while orienteering. Basically, let's say you are standing at the lower left corner of that triangle and you want to find the distance to a tower or other landmark (which would be side (a) in the example. What you would do is starting walking left or right about 200 or more yards or so away from that line (which is shown as "7" in the example, and you would measure the angle to the target from your new position using your compass (which is shown as "53" in the example. You would then use the tangent table to calculate the side "a" which gives you the distance to the landmark.
I don't recommend using tangent calculations by themselves though. If you're going to do advanced orienteering using trigonometry, you need to combine it with maps, time, compass, wind direction, Sun/Moon/Planets, beads (or other counting methods), altitude, temperature, etc. Using trig is only a small part of the whole and it shouldn't be used as a primary tool, only as a secondary tool to support what you see on your map and compass.